Scoop du Jour: Barycentric Quad Rasterization on a Cone

by C.G. Scoop

Sept., 2022

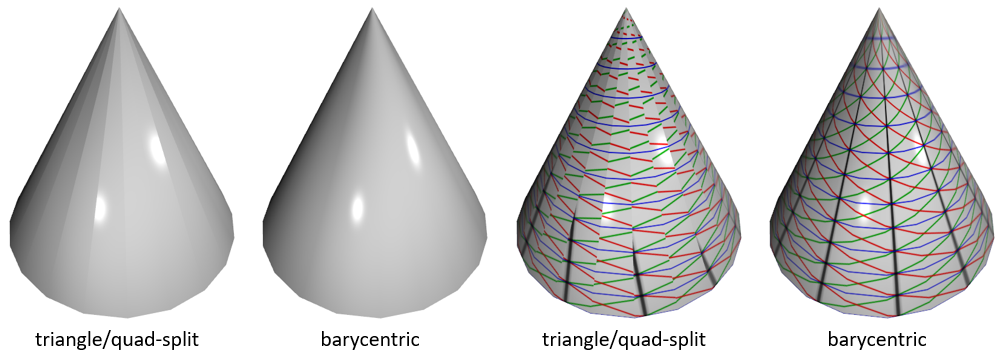
Last month, shortly after the Journal of Computer Graphics Techniques published Barycentric Quad Rasterization, Paul Haeberli asked whether the barycentric method, which reduces distortion and discontinuity in a texture-mapped sphere, could also improve the rendering of a cone? Yes, it can.

At the tip of a cone, as at a pole of a sphere, a quad has a degenerate edge defined by two coincident points (see Figure 6 of the paper). With triangle rasterization, one of the points is ignored (see Figure 7). For the sphere, the two points differ in uv-coordinates and thus triangle rasterization produces a texture discontinuity. For the cone, however, the two points also differ in surface normal, producing a shading discontinuity as well. This problem is discussed by Eric Haines in his 2014 post, Limits of Triangles.

The discontinuities in texture can be overcome by avoiding the Mercator projection used for a sphere and, instead, employing a conical projection as the texture source (that is, a circle whose circumference corresponds to the base of the cone and whose center corresponds to the tip). The discontinuities in shading, however, cannot be overcome with triangles or quad-splits.

Correction

The cone example revealed a bug in the pixel shader (Listing 2). In subroutine BarycentricWeights, the following assignment fails if A is zero:
t[i] = (r[i]*r[(i+1)%4]-D)/A;

It should be replaced with:
t[i] = abs(A) < 1.e-6? 0 : (r[i]*r[(i+1)%4]-D)/A;

This correction removes the need for double precision in the subroutines BarycentricWeights and UV (thus, p. 73, “Double precision is used ... artifacts” is incorrect).