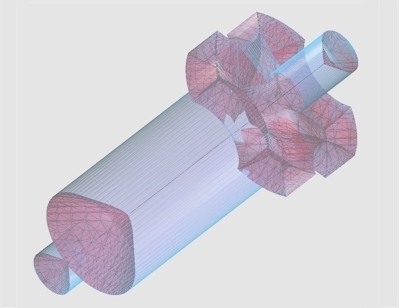
The medial axis/surface of a
three-dimensional object is the object’s ‘center’ (more formally,
the centers of maximally-inscribable spheres). The medial of a
sphere is its center; the medial of a cylinder is its axis. For
other objects, the medial is a collection of surfaces and/or arcs
that meet at non-manifold points and seams. The medial and the
object are intrinsically related: the object unambiguously defines
the medial, and the medial (and associated radii) can reconstruct
the object.
There are numerous applications for the
medial:
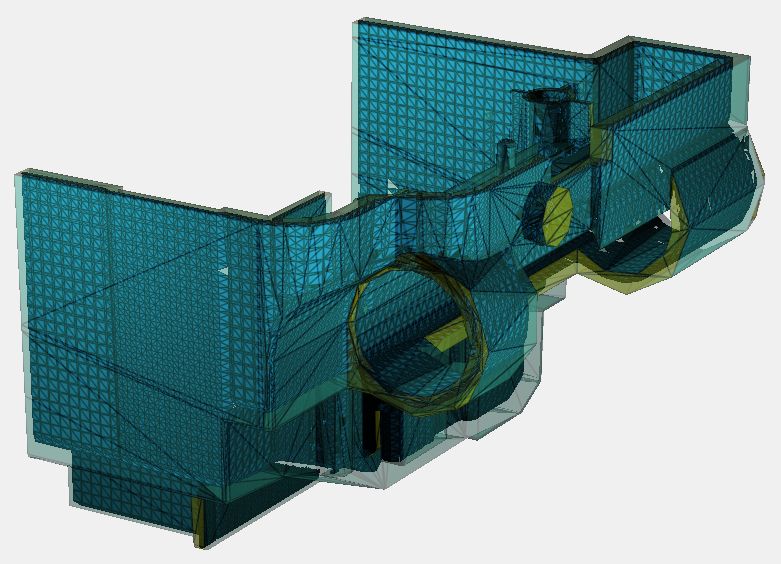
object partition before finite-element meshing, object
reconstruction from scattered points, collision detection,
robotic path planning, injection mold simulation, feature
recognition, character animation, biological landmark
measurement, level of detail representation, shape smoothing,
and shape metamorphosis.
Despite these varied
applications, software to compute the medial is largely
unavailable, due to the difficulty in computing the complex,
non-manifold geometry typical of the medial.
Unchained Geometry uses a
novel method to compute the medial: it is accurate to arbitrary
(user-settable) precision and robust for objects defined as
polyhedra, curved surfaces, or point-clouds. 1D medial
arcs and 2D medial surfaces are produced, with the result
explicitly representing non-manifold seams and their connections
to impinging surfaces. The method allows pruning of noisy parts of
the medial that result from irregularities in the input object.
The method requires only
modest memory, and computation time is on the order of the
medial's surface area, not the object's volume.
Unchained
Geometry's medial extraction method is patented (no. 6956565) in
2005.
Applications
of
the Medial Axis to Animation, publications
Medial-Based
Vertex Deformation (Symposium on Computer Animation)
Skeletal Methods of Shape Manipulation
(invited paper, Shape Modeling Int'l)